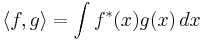Orthogonal functions

In mathematics, two functions $f$ and $g$ are called orthogonal if their inner product $\langle f,g\rangle$ is zero for f ≠ g. Whether or not two particular functions are orthogonal depends on how their inner product has been defined. A typical definition of an inner product for functions is

$\langle f,g\rangle = \int f^*(x) g(x)\,dx$

with appropriate integration boundaries. Here, the star is the complex conjugate.

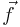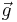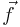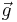For an intuitive perspective on this inner product, suppose approximating vectors $\vec{f}$ and $\vec{g}$ are created whose entries are the values of the functions f and g, sampled at equally spaced points. Then this inner product between f and g can be roughly understood as the dot product between approximating vectors $\vec{f}$ and $\vec{g}$ , in the limit as the number of sampling points goes to infinity. Thus, roughly, two functions are orthogonal if their approximating vectors are perpendicular (under this common inner product).[1]

See also Hilbert space for a more rigorous background.

Solutions of linear differential equations with boundary conditions can often be written as a weighted sum of orthogonal solution functions (a.k.a. eigenfunctions).

Examples of sets of orthogonal functions:

Generalization of vectors

It can be shown that orthogonality of functions is a generalization of the concept of orthogonality of vectors. Suppose we define V to be the set of variables on which the functions f and g operate. (In the example above, V={x} since x is the only parameter to f and g. Since there is one parameter, one integral sign is required to determine orthogonality. If V contained two variables, it would be necessary to integrate twice--over a range of each variable--to establish orthogonality.) If V is an empty set, then f and g are just constant vectors, and there are no variables over which to integrate. Thus, the equation reduces to a simple inner-product of the two vectors.